Creating a Full Sun Map with AIA and EUVI

With SDO/AIA and STEREO/A and STEREO/B, it is possible (for specific dates) to combine combine three EUV images from these satellites to produce a nearly full latitude / longitude map of the Sun.

You will need reproject v0.6 or higher installed.

import matplotlib.pyplot as plt
import numpy as np
from reproject import reproject_interp
from reproject.mosaicking import reproject_and_coadd

import astropy.units as u
from astropy.coordinates import SkyCoord
from astropy.wcs import WCS

import sunpy.map
import sunpy.sun
from sunpy.coordinates import get_body_heliographic_stonyhurst
from sunpy.data.sample import AIA_193_JUN2012, STEREO_A_195_JUN2012, STEREO_B_195_JUN2012

First create a sunpy map for each of the files.

maps = sunpy.map.Map(sorted([AIA_193_JUN2012, STEREO_A_195_JUN2012, STEREO_B_195_JUN2012]))

To reduce memory consumption we also downsample these maps before continuing, you can disable this.

maps = [m.resample((1024, 1024)*u.pix) for m in maps]

When combining these images all three need to assume the same radius of the Sun for the data. The AIA images specify a slightly different value than the IAU 2015 constant. To avoid coordinate transformation issues we reset this here.

maps[0].meta['rsun_ref'] = sunpy.sun.constants.radius.to_value(u.m)

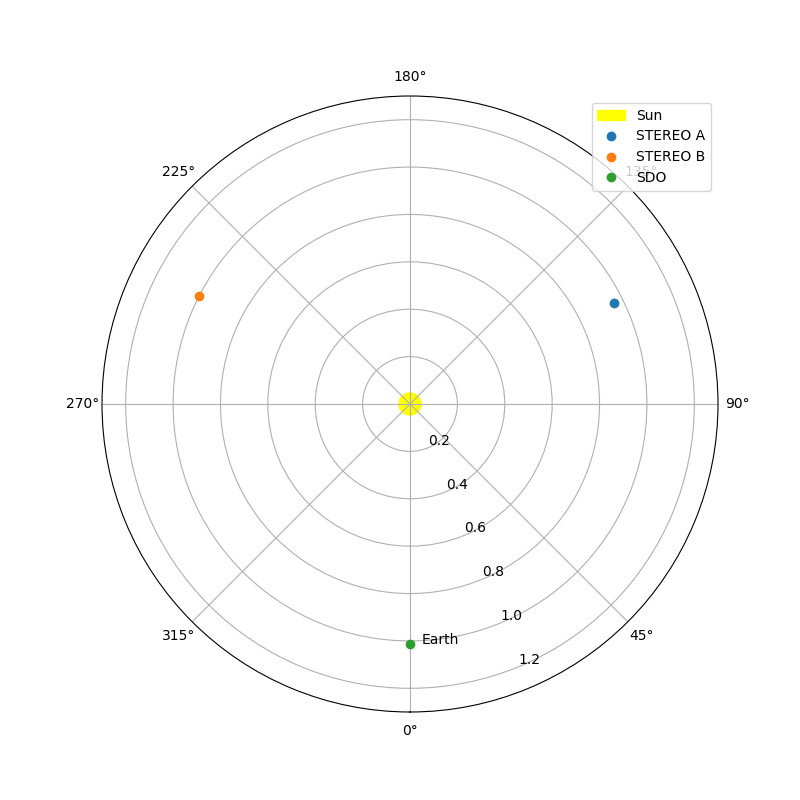
Next we will plot the locations of the three spacecraft with respect to the Sun so we can easily see the relative separations.

earth = get_body_heliographic_stonyhurst('earth', maps[0].date)

fig = plt.figure(figsize=(8, 8))
ax = fig.add_subplot(projection='polar')
circle = plt.Circle((0.0, 0.0), (10*u.Rsun).to_value(u.AU),
                    transform=ax.transProjectionAffine + ax.transAxes, color="yellow",
                    alpha=1, label="Sun")
ax.add_artist(circle)
ax.text(earth.lon.to_value("rad")+0.05, earth.radius.to_value(u.AU), "Earth")

for this_satellite, this_coord in [(m.observatory, m.observer_coordinate) for m in maps]:
    ax.plot(this_coord.lon.to('rad'), this_coord.radius.to(u.AU), 'o', label=this_satellite)

ax.set_theta_zero_location("S")
ax.set_rlim(0, 1.3)
ax.legend()

plt.show()

INFO: Missing metadata for solar radius: assuming the standard radius of the photosphere. [sunpy.map.mapbase]

The next step is to calculate the output coordinate system for the combined map. We select a heliographic Stonyhurst frame, and a Plate Carree (CAR) projection, and generate a header using sunpy.map.header_helper.make_fitswcs_header and then construct a World Coordinate System (WCS) object for that header.

shape_out = (180, 360)  # This is set deliberately low to reduce memory consumption
header = sunpy.map.make_fitswcs_header(shape_out,
                                       SkyCoord(0, 0, unit=u.deg,
                                                frame="heliographic_stonyhurst",
                                                obstime=maps[0].date),
                                       scale=[360 / shape_out[1],
                                              180 / shape_out[0]] * u.deg / u.pix,
                                       wavelength=int(maps[0].meta['wavelnth']) * u.AA,
                                       projection_code="CAR")
out_wcs = WCS(header)

Next we call the reproject.mosaicking.reproject_and_coadd function, which takes a list of maps, and the desired output WCS and array shape.

array, footprint = reproject_and_coadd(maps, out_wcs, shape_out,
                                       reproject_function=reproject_interp)

/home/docs/checkouts/readthedocs.org/user_builds/sunpy/conda/stable/lib/python3.10/site-packages/sunpy/coordinates/frames.py:614: SunpyUserWarning: The conversion of these 2D helioprojective coordinates to 3D is all NaNs because off-disk coordinates need an additional assumption to be mapped to calculate distance from the observer. Consider using the context manager `Helioprojective.assume_spherical_screen()`.
  warn_user("The conversion of these 2D helioprojective coordinates to 3D is all NaNs "
INFO: Missing metadata for solar radius: assuming the standard radius of the photosphere. [sunpy.map.mapbase]
/home/docs/checkouts/readthedocs.org/user_builds/sunpy/conda/stable/lib/python3.10/site-packages/sunpy/coordinates/frames.py:614: SunpyUserWarning: The conversion of these 2D helioprojective coordinates to 3D is all NaNs because off-disk coordinates need an additional assumption to be mapped to calculate distance from the observer. Consider using the context manager `Helioprojective.assume_spherical_screen()`.
  warn_user("The conversion of these 2D helioprojective coordinates to 3D is all NaNs "
/home/docs/checkouts/readthedocs.org/user_builds/sunpy/conda/stable/lib/python3.10/site-packages/sunpy/coordinates/frames.py:614: SunpyUserWarning: The conversion of these 2D helioprojective coordinates to 3D is all NaNs because off-disk coordinates need an additional assumption to be mapped to calculate distance from the observer. Consider using the context manager `Helioprojective.assume_spherical_screen()`.
  warn_user("The conversion of these 2D helioprojective coordinates to 3D is all NaNs "

To display the output we construct a new map using the new array and our generated header. We also borrow the plot settings from the AIA map.

outmap = sunpy.map.Map((array, header))
outmap.plot_settings = maps[0].plot_settings

fig = plt.figure()
ax = fig.add_subplot(projection=outmap)
outmap.plot(axes=ax)

plt.show()

Improving the Output

As you can see this leaves a little to be desired. To reduce the obvious warping towards the points which are close to the limb in the input images, we can define a set of weights to use when co-adding the output arrays. To reduce this warping we want to calculate an set of weights which highly weigh points close to the centre of the disk in the input image.

We can achieve this by using sunpy’s coordinate framework. First we calculate all the world coordinates for all the pixels in all three input maps.

coordinates = tuple(map(sunpy.map.all_coordinates_from_map, maps))

To get a weighting which is high close to disk centre and low towards the limb, we can use the Z coordinate in the heliocentric frame. This coordinate is the distance of the sphere from the centre of the Sun towards the observer.

weights = [coord.transform_to("heliocentric").z.value for coord in coordinates]

These weights are good, but they are better if the ramp down is a little smoother, and more biased to the centre. Also we can scale them to the range 0-1, and set any off disk (NaN) regions to 0.

weights = [(w / np.nanmax(w)) ** 3 for w in weights]
for w in weights:
    w[np.isnan(w)] = 0

fig, ax = plt.subplots()
im = ax.imshow(weights[0])
fig.colorbar(im)

plt.show()

Now we can rerun the reprojection. This time we also set match_background=True which scales the images by a single scaling factor so they are of similar brightness. We also set background_reference=0 which uses the AIA map as the reference for the background scaling.

Here we are using the fastest but least accurate method of reprojection, reproject.reproject_interp, a more accurate but slower method is reproject.reproject_adaptive.

array, _ = reproject_and_coadd(maps, out_wcs, shape_out,
                               input_weights=weights,
                               reproject_function=reproject_interp,
                               match_background=True,
                               background_reference=0)

/home/docs/checkouts/readthedocs.org/user_builds/sunpy/conda/stable/lib/python3.10/site-packages/sunpy/coordinates/frames.py:614: SunpyUserWarning: The conversion of these 2D helioprojective coordinates to 3D is all NaNs because off-disk coordinates need an additional assumption to be mapped to calculate distance from the observer. Consider using the context manager `Helioprojective.assume_spherical_screen()`.
  warn_user("The conversion of these 2D helioprojective coordinates to 3D is all NaNs "
/home/docs/checkouts/readthedocs.org/user_builds/sunpy/conda/stable/lib/python3.10/site-packages/sunpy/coordinates/frames.py:614: SunpyUserWarning: The conversion of these 2D helioprojective coordinates to 3D is all NaNs because off-disk coordinates need an additional assumption to be mapped to calculate distance from the observer. Consider using the context manager `Helioprojective.assume_spherical_screen()`.
  warn_user("The conversion of these 2D helioprojective coordinates to 3D is all NaNs "
/home/docs/checkouts/readthedocs.org/user_builds/sunpy/conda/stable/lib/python3.10/site-packages/sunpy/coordinates/frames.py:614: SunpyUserWarning: The conversion of these 2D helioprojective coordinates to 3D is all NaNs because off-disk coordinates need an additional assumption to be mapped to calculate distance from the observer. Consider using the context manager `Helioprojective.assume_spherical_screen()`.
  warn_user("The conversion of these 2D helioprojective coordinates to 3D is all NaNs "

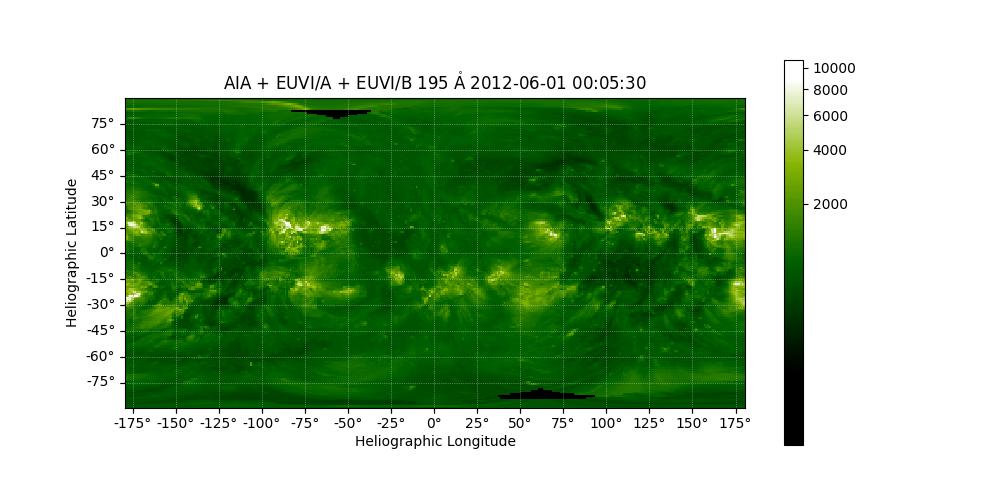
Once again we create a new map, and this time we customise the plot a little.

outmap = sunpy.map.Map((array, header))
outmap.plot_settings = maps[0].plot_settings
outmap.nickname = 'AIA + EUVI/A + EUVI/B'

fig = plt.figure(figsize=(10, 5))
ax = fig.add_subplot(projection=outmap)
im = outmap.plot(axes=ax, vmin=400)

lon, lat = ax.coords
lon.set_coord_type("longitude")
lon.coord_wrap = 180 * u.deg
lon.set_format_unit(u.deg)
lat.set_coord_type("latitude")
lat.set_format_unit(u.deg)

lon.set_axislabel('Heliographic Longitude', minpad=0.8)
lat.set_axislabel('Heliographic Latitude', minpad=0.9)
lon.set_ticks(spacing=25*u.deg, color='k')
lat.set_ticks(spacing=15*u.deg, color='k')

plt.colorbar(im, ax=ax)

# Reset the view to pixel centers
_ = ax.axis((0, shape_out[1], 0, shape_out[0]))

plt.show()