Compensating for Solar Rotation

Often a set of solar image data consists of fixing the pointing of a field of view for some time and observing. Features on the Sun will differentially rotate depending on latitude, with features at the equator moving faster than features at the poles.

In this example, the process of shifting images in a MapSequence to account for the differential rotation of the Sun is demonstrated using the mapsequence_coalign_by_rotation() function.

import matplotlib.pyplot as plt
import sunpy.data.sample
from sunpy.map import Map

from sunkit_image import coalignment

First, create a MapSequence with sample data.

mc = Map(
    [
        sunpy.data.sample.AIA_193_CUTOUT01_IMAGE,
        sunpy.data.sample.AIA_193_CUTOUT02_IMAGE,
        sunpy.data.sample.AIA_193_CUTOUT03_IMAGE,
        sunpy.data.sample.AIA_193_CUTOUT04_IMAGE,
        sunpy.data.sample.AIA_193_CUTOUT05_IMAGE,
    ],
    sequence=True,
)

Files Downloaded:   0%|          | 0/1 [00:00<?, ?file/s]

AIA20110607_063307_0193_cutout.fits:   0%|          | 0.00/1.45M [00:00<?, ?B/s]

AIA20110607_063307_0193_cutout.fits:  80%|████████  | 1.16M/1.45M [00:00<00:00, 11.3MB/s]


Files Downloaded: 100%|██████████| 1/1 [00:00<00:00,  4.38file/s]
Files Downloaded: 100%|██████████| 1/1 [00:00<00:00,  4.37file/s]

Files Downloaded:   0%|          | 0/1 [00:00<?, ?file/s]

AIA20110607_063931_0193_cutout.fits:   0%|          | 0.00/1.45M [00:00<?, ?B/s]


Files Downloaded: 100%|██████████| 1/1 [00:00<00:00,  4.34file/s]
Files Downloaded: 100%|██████████| 1/1 [00:00<00:00,  4.33file/s]

Files Downloaded:   0%|          | 0/1 [00:00<?, ?file/s]

AIA20110607_064555_0193_cutout.fits:   0%|          | 0.00/1.45M [00:00<?, ?B/s]

AIA20110607_064555_0193_cutout.fits:  60%|██████    | 874k/1.45M [00:00<00:00, 8.42MB/s]


Files Downloaded: 100%|██████████| 1/1 [00:00<00:00,  5.11file/s]
Files Downloaded: 100%|██████████| 1/1 [00:00<00:00,  5.09file/s]

Files Downloaded:   0%|          | 0/1 [00:00<?, ?file/s]

AIA20110607_065219_0193_cutout.fits:   0%|          | 0.00/1.46M [00:00<?, ?B/s]

AIA20110607_065219_0193_cutout.fits:  80%|████████  | 1.17M/1.46M [00:00<00:00, 11.4MB/s]


Files Downloaded: 100%|██████████| 1/1 [00:00<00:00,  4.78file/s]
Files Downloaded: 100%|██████████| 1/1 [00:00<00:00,  4.77file/s]

Files Downloaded:   0%|          | 0/1 [00:00<?, ?file/s]

AIA20110607_065843_0193_cutout.fits:   0%|          | 0.00/1.45M [00:00<?, ?B/s]

AIA20110607_065843_0193_cutout.fits:  80%|████████  | 1.16M/1.45M [00:00<00:00, 10.9MB/s]


Files Downloaded: 100%|██████████| 1/1 [00:00<00:00,  3.66file/s]
Files Downloaded: 100%|██████████| 1/1 [00:00<00:00,  3.65file/s]

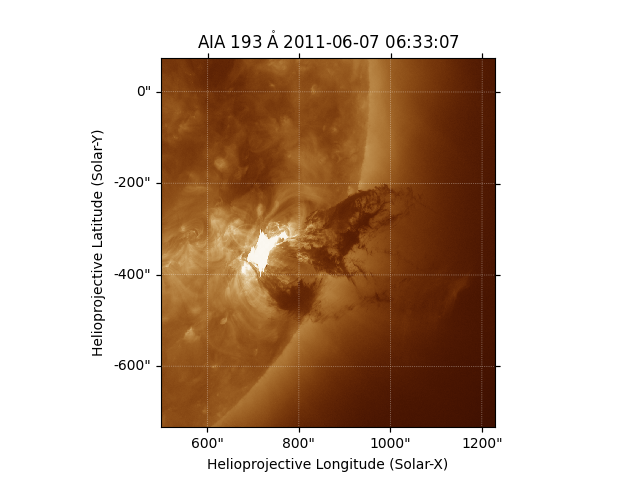
Let’s plot the MapSequence so we can later compare it with the shifted result.

plt.figure()
anim = mc.plot()

The mapsequence_coalign_by_rotation() function can be applied to the Map Sequence

derotated = coalignment.mapsequence_coalign_by_rotation(mc)

By default, the de-rotation shifts are calculated relative to the first map in the MapSequence. This function does not differentially rotate the image (see Differentially rotating a map for an example). It is useful for de-rotating images when the effects of differential rotation in the MapSequence can be ignored.

See the docstring of mapsequence_coalign_by_rotation() for more features of the function.

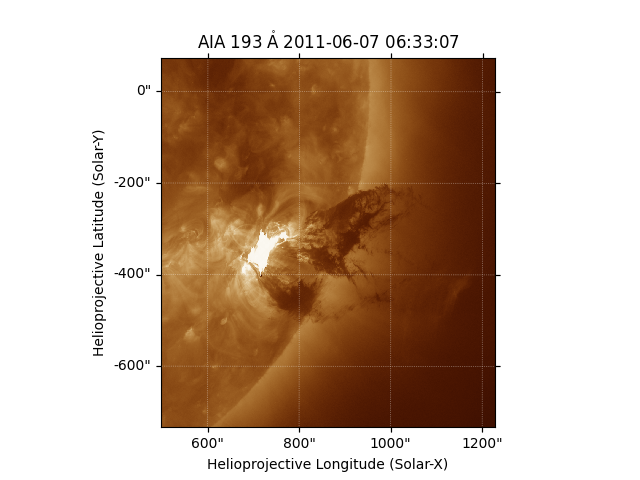
To check that the applied shifts were reasonable, plot an animation of the shifted MapSequence to compare with the original plot above.

plt.figure()
anim_derotate = derotated.plot()

The de-rotation shifts used in the above function can be calculated without applying them using the calculate_solar_rotate_shift() function.

shifts = coalignment.calculate_solar_rotate_shift(mc)

The calculated shifts can be passed as an argument to mapsequence_coalign_by_rotation().

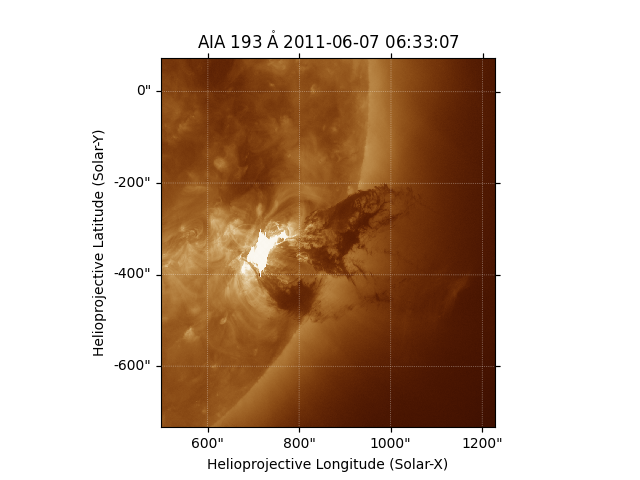
derotate_shifts = coalignment.mapsequence_coalign_by_match_template(mc, shift=shifts)

plt.figure()
anim_derotate_shifts = derotate_shifts.plot()

plt.show()