Saving and loading coordinates with asdf

In this example we are going to look at saving and loading collections of coordinates with asdf.

asdf is a modern file format designed to meet the needs of the astronomy community. It has deep integration with Python and sunpy and Astropy as well as implementations in other languages. It can be used to store known Python objects in a portable, well defined file format. It is primarily useful for storing complex Astropy and SunPy objects in a way that can be loaded back into the same form as they were saved.

Note

This example requires astropy>=3.2 and asdf>=2.3.0

import matplotlib.pyplot as plt
import numpy as np

import asdf
import astropy.units as u
from astropy.coordinates import SkyCoord

import sunpy.map
from sunpy.coordinates import frames
from sunpy.data.sample import AIA_171_IMAGE
from sunpy.sun import constants

To get started let’s use a function to get the coordinates of a semi-circular loop from this blog post by Will Barnes to generate ourselves some coordinates.

@u.quantity_input
def semi_circular_loop(length: u.cm, latitude: u.deg = 0*u.deg):
    """
    Return HGS coordinates for a semi-circular loop
    """
    angles = np.linspace(0, 1, 1000) * np.pi * u.rad
    z = length / np.pi * np.sin(angles)
    x = length / np.pi * np.cos(angles)
    hcc_frame = frames.Heliocentric(
        observer=frames.HeliographicStonyhurst(lon=0 * u.deg, lat=latitude, radius=constants.au))

    return SkyCoord(
        x=x,
        y=np.zeros_like(x),
        z=z + constants.radius,
        frame=hcc_frame)

Use this function to generate a SkyCoord object.

loop_coords = semi_circular_loop(500*u.Mm, 30*u.deg)
print(loop_coords.shape)
# print the first and last coordinate point
print(loop_coords[[0, -1]])

(1000,)
<SkyCoord (Heliocentric: obstime=None, observer=<HeliographicStonyhurst Coordinate (obstime=None, rsun=695700.0 km): (lon, lat, radius) in (deg, deg, m)
    (0., 30., 1.49597871e+11)>): (x, y, z) in Mm
    [( 159.15494309, 0., 695.7), (-159.15494309, 0., 695.7)]>

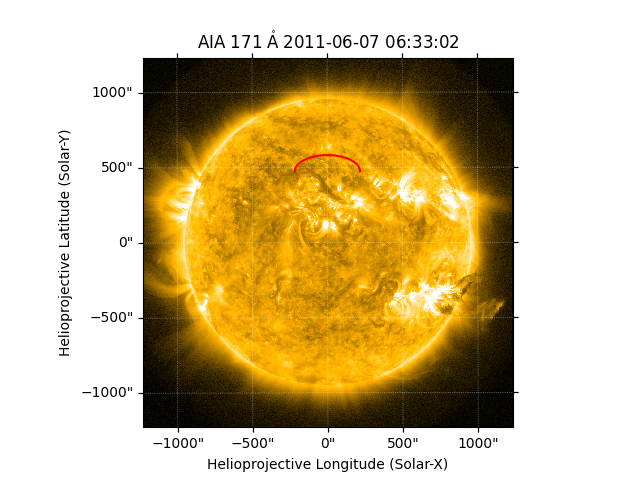
This is a regular coordinate object that can be transformed to other frames or overplotted on images. For instance we could overplot it on an AIA image

aiamap = sunpy.map.Map(AIA_171_IMAGE)

fig = plt.figure()
ax = fig.add_subplot(projection=aiamap)
aiamap.plot(axes=ax, clip_interval=(1, 99.5) * u.percent)
ax.plot_coord(loop_coords, 'r')

plt.show()

We can now save these loop points to an asdf file to use later. The advantage of saving them to asdf is that all the metadata about the coordinates will be preserved, and when we load the asdf, we will get back an identical SkyCoord object.

asdf files save a dictionary to a file, so to save the loop coordinates we need to put them into a dictionary. This becomes what asdf calls a tree.

tree = {'loop_points': loop_coords}

with asdf.AsdfFile(tree) as asdf_file:
    asdf_file.write_to("loop_coords.asdf")

This asdf file is a portable file and can be safely loaded by anyone with Astropy and sunpy installed. We can reload the file like so:

with asdf.open("loop_coords.asdf") as input_asdf:
    new_coords = input_asdf['loop_points']

print(new_coords.shape)
# print the first and last coordinate point
print(new_coords[[0, -1]])

(1000,)
<SkyCoord (Heliocentric: obstime=None, observer=<HeliographicStonyhurst Coordinate (obstime=None, rsun=695700.0 km): (lon, lat, radius) in (deg, deg, m)
    (0., 30., 1.49597871e+11)>): (x, y, z) in Mm
    [( 159.15494309, 0., 695.7), (-159.15494309, 0., 695.7)]>